Yu Zhang

Website

Hybrid Trajectory Planning for Autonomous Driving in Highly Constrained Environments

Yu Zhang1,Huiyan Chen1,Steven L. Waslander2, Jianwei Gong1, Guangming Xiong1, Tian Yang1, Kai Liu1
1Beijing Institute of Technology,2University of Toronto

PaperCodeArxivVideoData

Highlights

Background

In general, a trajectory planning problem refers to finding an optimal path with time stamped positions, orientations, and velocities from the current configuration to the goal configuration by minimizing certain objectives subject to geometry constraints (feasible paths must lie in the free space), task constraints (requirements to visit certain intermediate targets), and nonholonomic constraints (vehicle kinematics and dynamics). This kind of problem is known to be PSPACE-hard, which means there is no polynomial-time algorithm able to solve all instances of the problem[1][2]. The compounding effect of geometry, task and and nonholonomic constraints (differential constraints) increases the difficulty of developing practical trajectory planning algorithms that directly solve the complete trajectory planning problem[3][4].

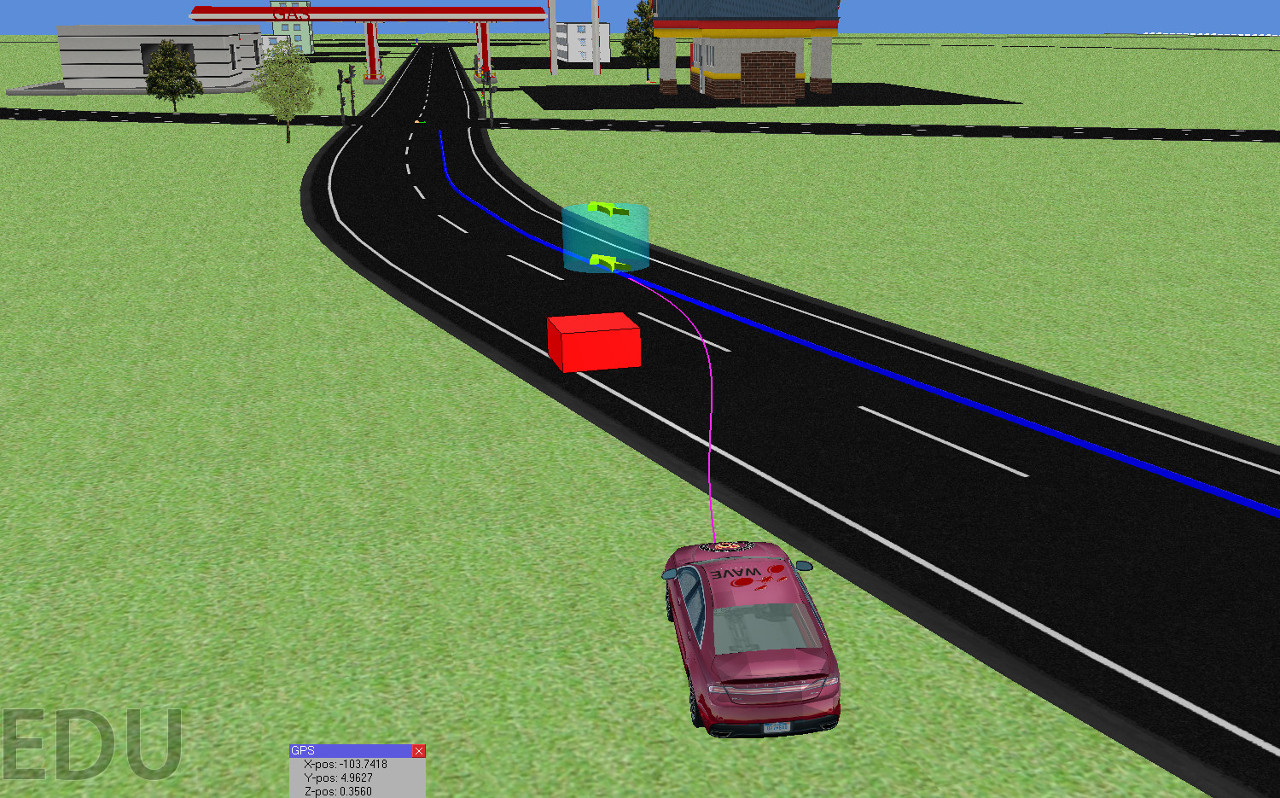
Our solution

In order to solve the motion planning problem in real time for autonomous driving, we propose a hybrid trajectory planning algorithm by combining the strengths of different methods. We assume the drivable region and the global path, which may be or may not be collision-free, are provided. As an optimization problem with both nonholonomic and geometry constraints is PSPACE-hard, the trajectory planning problem is decomposed into spatial path planning and speed planning sub-problems. The spatial path planning problem is further decomposed to a global path modification layer within the given drivable region and a multi-phase state space sampling planner layer. The speed planning sub-problem is solved by an optimization-based speed planning layer along the fixed path. In this way, the combinatorial constraints of the motion planning problems are separated, which is convenient to address different constraints by taking advantages of different methods. Besides, the decomposition makes the planner be able to limit the search space by leveraging the constraint information while still maintaining richness of the feasible solution space in different layers.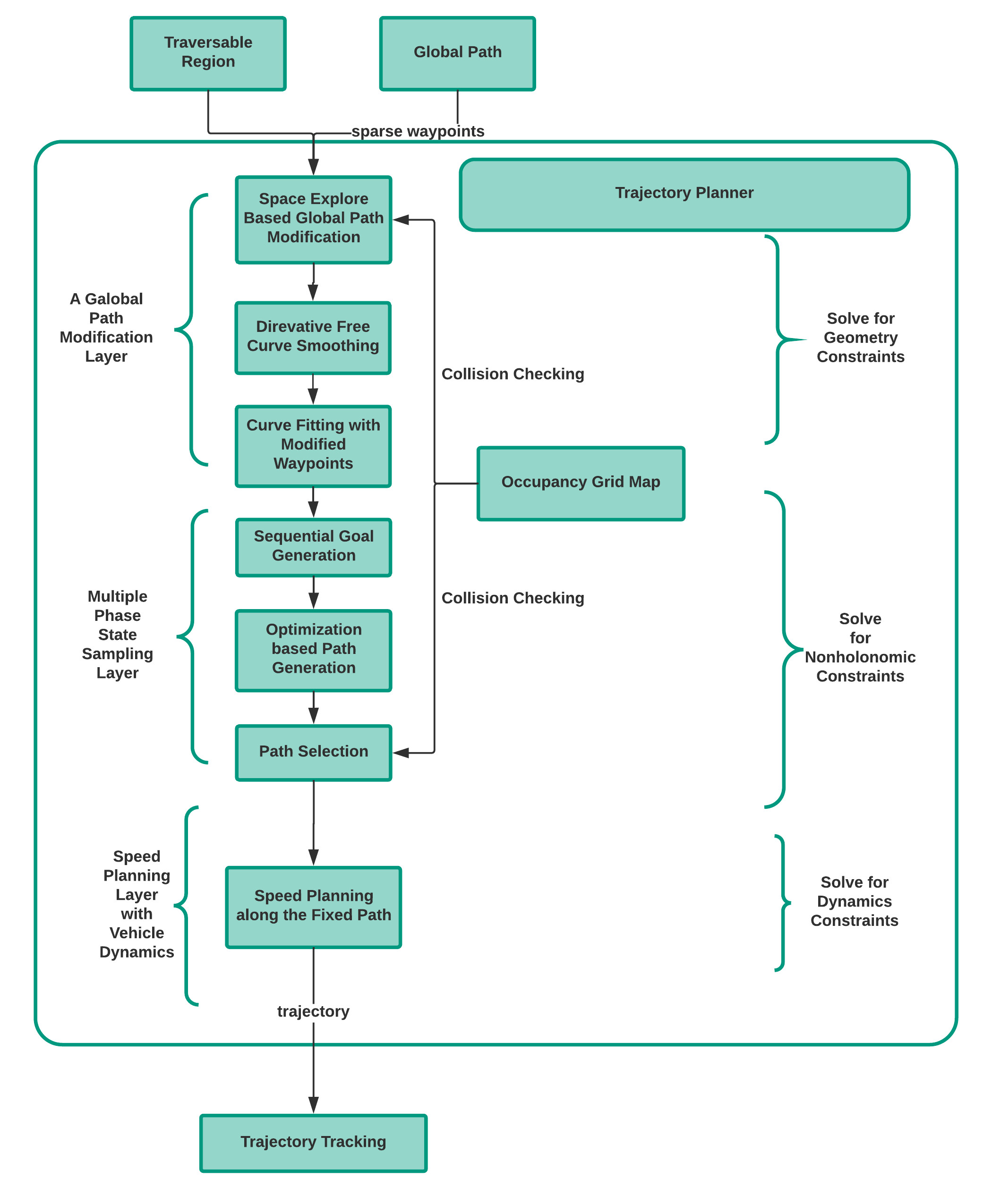

Hybrid motion planning framework.

Highlights

We

  • Present a novel and efficient trajectory planning framework that is able to handle geometry constraints, nonholonomic constraints and dynamics constraints of cars in a human-like and layered fashion and generate curvature-continuous, kinodynamically feasible, smooth and collision-free trajectories in real-time.
  • Develop a derivative-free global path modification algorithm to extract high-order state information in free space for state sampling.
  • Extend the regular state space sampling method widely used in on-road autonomous driving systems to a multi-phase deterministic state space sampling method that is able to approximate complex maneuvers.
  • Improve collision checking accuracy and efficiency by using a different car footprint approximation strategy and a two-phase collision checking routine.

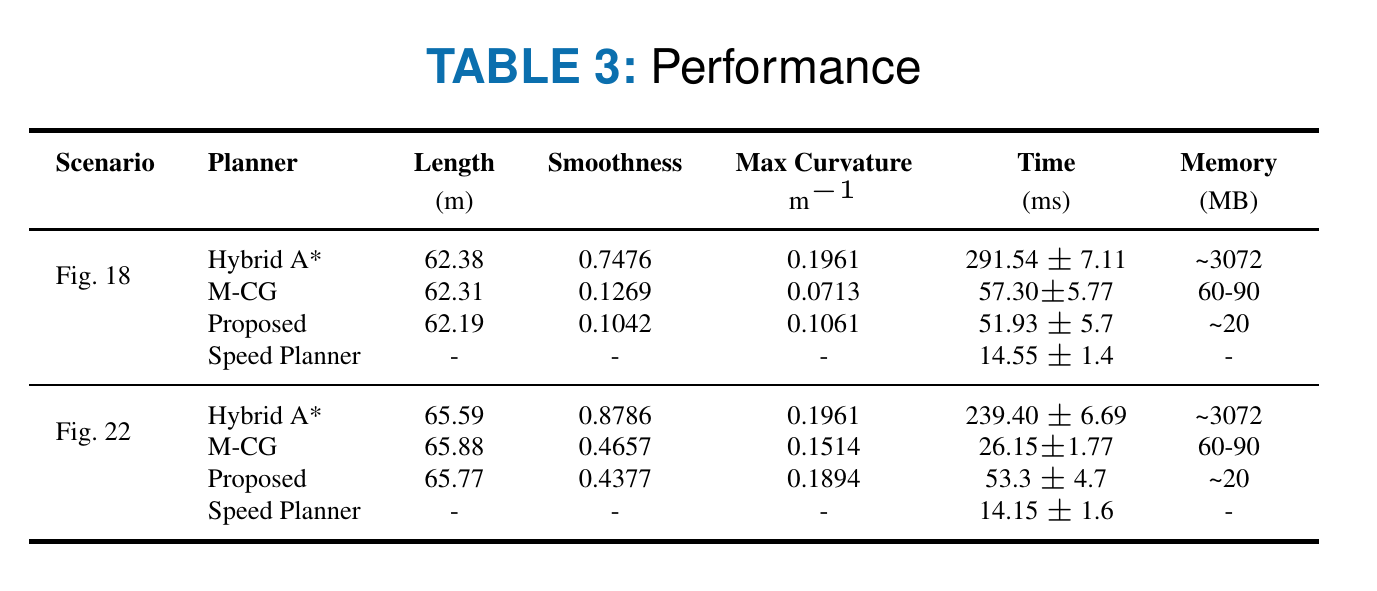
A range of challenging simulation experiments show that the proposed method returns high quality trajectories in real-time and outperforms existing planners such as hybrid A*, conjugate-gradient descent path smoother in terms of path quality, efficiency and computation resources used. Please see our paper[5] for details.

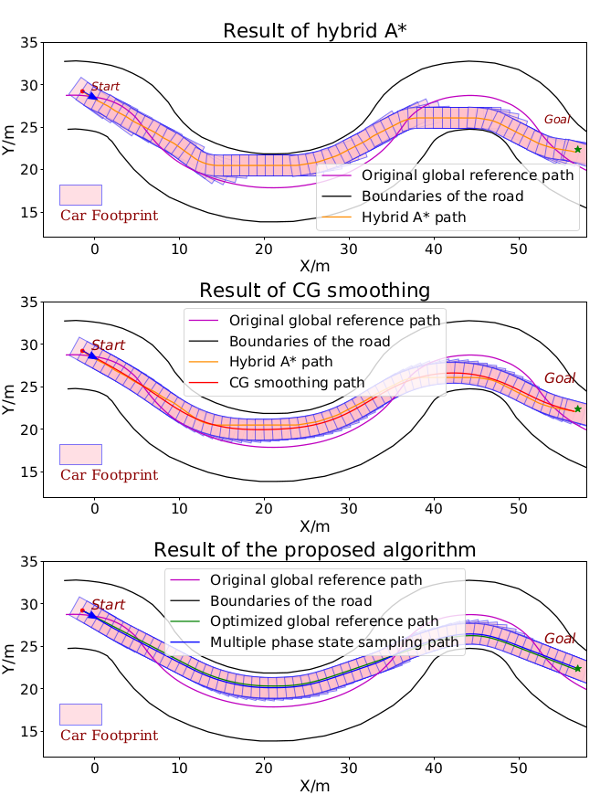
without obstacles
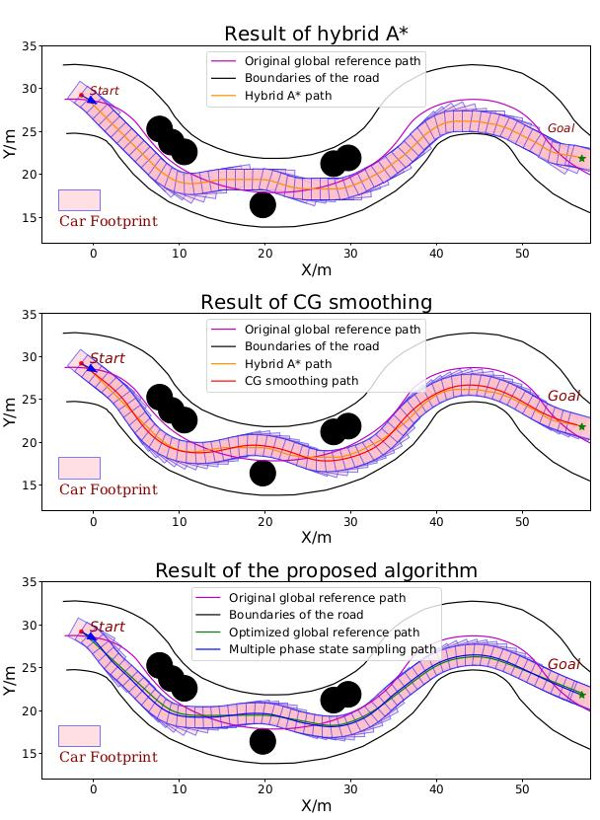
with obstacles
Comparison of Performance. Smoothness: the lower, the better.

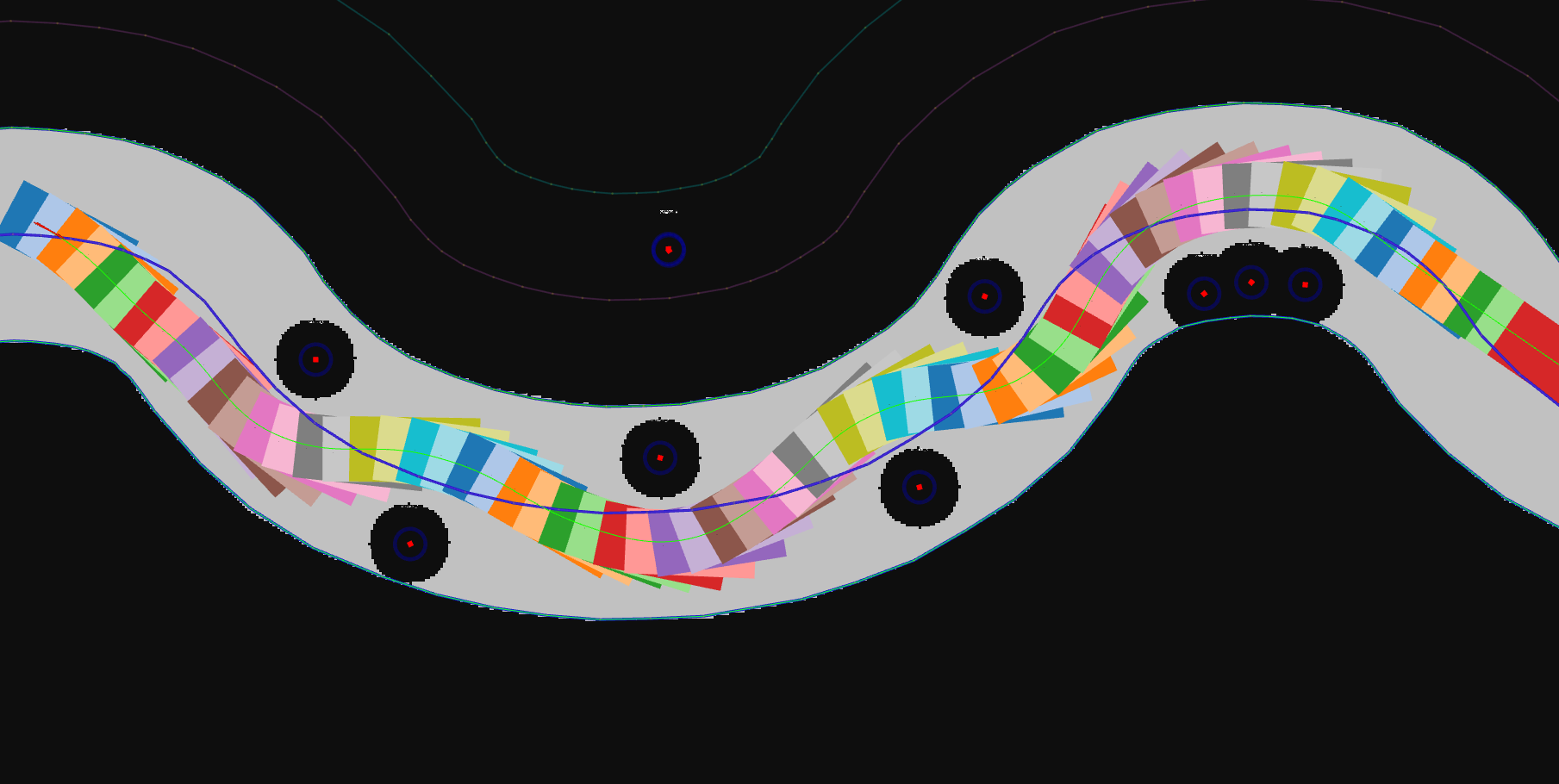
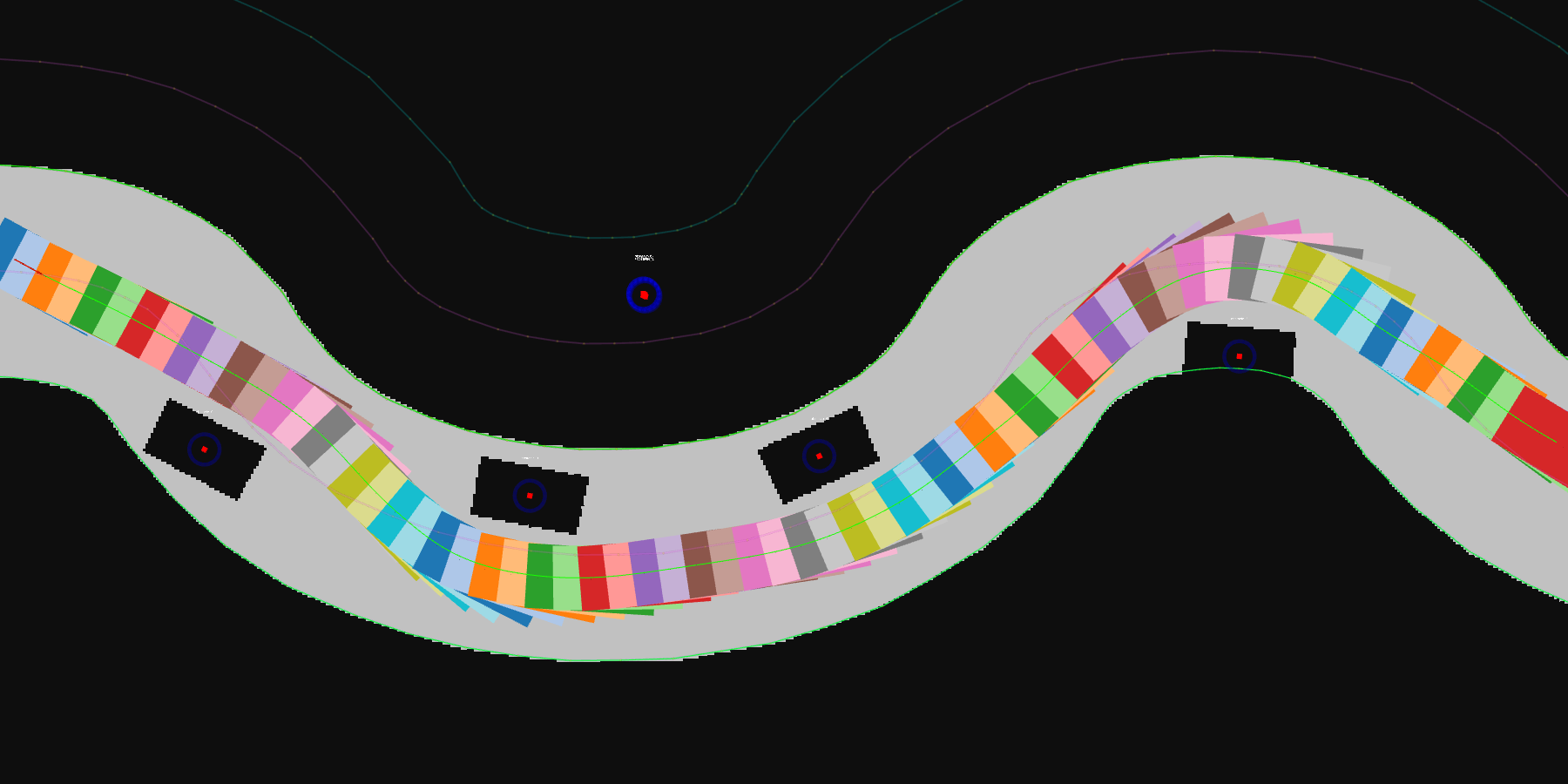
Other Scenarios

scene1
scene2
scene3

BibTeX

@article{zhang2018hmpl,
  author = {Zhang, Yu and Chen, Huiyan and Waslander, Steven L. and Gong, Jianwei and Xiong, Guangming and Yang, Tian and Liu, Kai},
  title = {{Hybrid Trajectory Planning for Autonomous Driving in Highly Constrained Environments}},
  journal={IEEE Access},
  year = {2018},
  doi={10.1109/ACCESS.2018.2845448},
  pages={32800-32819},
  volume={6},
  publisher={IEEE}
}

References

  1. 1.John H Reif, “Complexity of the mover’s problem and generalizations,” in IEEE Annual Symposium on Foundations of Computer Science (FOCS), 1979, pp. 421–427. ↩
  2. 2.Brian Paden, Michal Čáp, Sze Zheng Yong, Dmitry Yershov, and Emilio Frazzoli, “A Survey of Motion Planning and Control Techniques for Self-driving Urban Vehicles,” IEEE Transactions on Intelligent Vehicles, vol. 1, no. 1, pp. 33–55, 2016. ↩
  3. 3.Jerome Barraquand and J-C Latombe, “On nonholonomic mobile robots and optimal maneuvering,” in IEEE International Symposium on Intelligent Control (ISIC), 1989, pp. 340–347. ↩
  4. 4.Bai Li and Zhijiang Shao, “Simultaneous dynamic optimization: A trajectory planning method for nonholonomic car-like robots,” Advances in Engineering Software, vol. 87, pp. 30–42, 2015. ↩
  5. 5.Yu Zhang, Huiyan Chen, Steven L. Waslander, Jianwei Gong, Guangming Xiong, Tian Yang, and Kai Liu, “Hybrid Trajectory Planning for Autonomous Driving in Highly Constrained Environments,” IEEE Access, vol. 6, pp. 32800–32819, 2018. ↩
0%